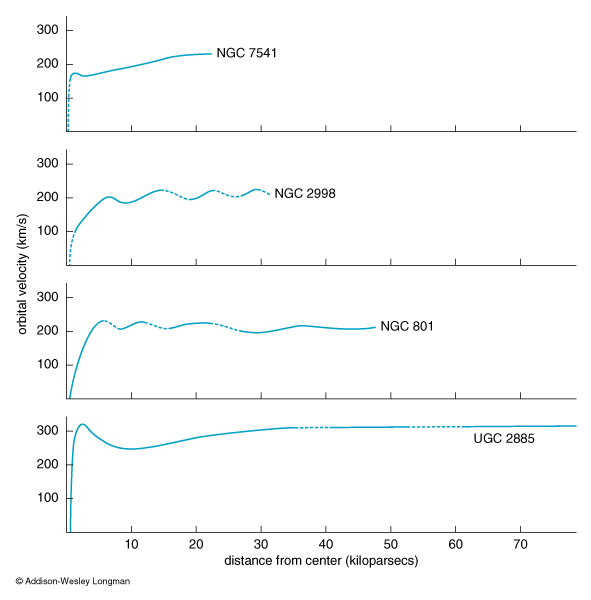
Determining the Mass of a Spherical Mass Distribution Inside
a Given Radius Ro
A. The gravitational effects of a thin spherical
shell of mass:
1. Outside a thin shell of mass, the gravitational force of the shell
acts on any object as if the force comes from the center and is proportional
to the total mass of the shell and is inversely proportional to the square
of the distance from the center. (ie: Obeys Newton's
universal law of gravity: F = Gmshellmobject/r2;
where G = universal gravity constant, m = mass of shell or object [labeled],
r = dist. from center of spherical shell to object outside shell)
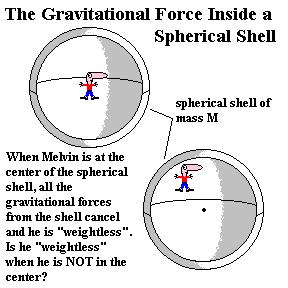
2. Inside the shell of mass, the gravitational forces of the different
portions of the shell cancel each other out exactly so that an object
interior to the shell feels no gravitaional force from the shell.
(ie: Net gravity force = 0, no matter where it is inside the spherical
shell.)
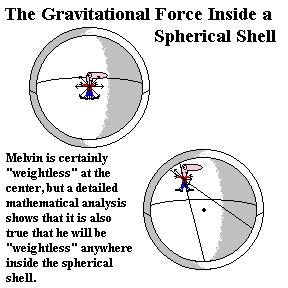
3. Since a thick spherical shell can be modeled as concentric thin
shells, it follows that within a concentric spherical space in the middle
of a spherical distribution of mass the net gravitational force on an
object will be zero.
B. The gravitational effects of a spherical mass distribution:
the gravitational force outside the distribution obeys Newton's universal
law of gravity exactly as for a spherical shell of mass (see A.1. above)
such that the gravitational force of the spherical mass distribution acts
on any object outside the distribution as if the force comes from the center
of the distribution and is proportional to the total mass of the distribution
and is inversely proportional to the square of the distance from the center.
C. Now assume an object of mass mobject
in a circular orbit inside a spherical mass distribution with a radius
of Ro with a mass inside the radius Ro designated
by MRo (eg:
a spherical distribution of stars with the object = a star orbiting in
a circular orbit with radius Ro inside the distribution of other
stars)
1. there is no net gravitational force from the mass distribution
outside the radius Ro (a thick spherical shell) 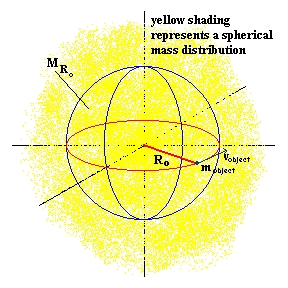
2. the net gravitational force on the object comes from the spherical
mass distribution inside the orbital radius Ro and is described
by the universal gravity law: Fnet
= GmobjectMRo/Ro2
3. by Newton's 2nd law and his definition of centripetal acceleration
we can write:
mobjectv2object
= GmobjectMRo/Ro2
[note: v2object
= square of the orbital velocity]
canceling out the object's mass and solving for MRo
(mass
interior to Ro) we get the following equation: 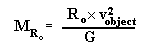
D. if the orbital velocity as
a function of radius can be measured [v = v(r), the rotation curve], then
the above equation can be used to determine the total mass interior to
a radius r as a function of radius [M = M(r)]: