1.  before distances could be measured to even the closest stars, the absolute scale of the solar system had to be determined; sometimes known as the "zeroth rung", the determination of the astronomical unit (1AU = average radius of the Earth's orbit) is the foundation on which the cosmic distance ladder rests

2.  the first step in determining interstellar distances is stellar parallax (see below); the following short non comprehensive overview lists some of the distance measuring techniques used in determining the cosmic distance scale:  (note on units:  one special astronomical unit of length that many people are familiar with is the light year (ly) = the distance light travels in 1 year, about 6 trillion miles; astronomers tend to use the distance unit known as a parsec (pc), note 1 pc = 3.26 ly and 1 kpc = 1000 pc = 3260 ly)

parallax - nearby stars (with recent HIPPARCOS satellite data, out to ~ 1kpc); spectroscopic parallax - stars with resolvable spectral type, mostly within 10 kpc; cluster main sequence fitting - star clusters within 15 kpc; cepheid pulsating variable stars - previously within the local group (galaxy cluster), now with Hubble Telescope out to Virgo Galaxy Cluster ~25,000 kpc; Type Ia supernova - galaxy clusters well beyond Virgo Cluster, several 100,000 kpc to perhaps a few million kpc in a few cases; Hubble's Law - theoretically anywhere within the observable universe if possible to measure a redshift

1.  using images taken 6 months apart, the apparent shift in angular position of a nearby star relative to background stars in the field of view may be measured, ½ of the angular shift is defined as the stellar parallax angle (P); the background stars must be many, many times further away than the nearby foreground star for the geometric assumptions to be valid; if the diagram below were actually to scale, the nearby star would be well over 2 miles to the right of the Sun for even the closest star to the Sun; then P would be extremely small and the small angle approximation holds allowing for the simple equation shown boxed in the diagram below

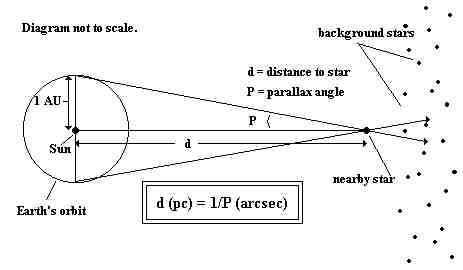
2.  the simple equation shown boxed in the above diagram must be used with the special units indicated in the parenthesis:  arcsec = "second of arc"  = angular unit, 1 arcsec = 1/3600 of a degree; pc = "parsec" = special distance unit defined as the distance a star would be if its measured parallax angle was exactly equal to 1 arcsec (hence, "parsec"); note:  since both light year and parsec sound somewhat like "time" units, many people confuse them with units of time - remember they are both units of length, NOT time

1.  doppler effect (see diagram):  the observed frequency and wavelength of light emitted from an object moving toward an observer is shifted to higher frequency and shorter wavelength ("blue-shifted") by the relative motion; for an object moving away from an observer the light is observed to shift to lower frequency and longer wavelength ("red-shifted"); in terms of wavelenght, the non-relativistic equation which describes the doppler effect is given by:

where v = relative velocity of the object emitting the light to the observer; c = speed of light; l = the measured wavelength of light from the moving object; l_o = the rest wavelength (ie:  the wavelength the light would be if the object were at rest relative to the observer)  {typically, the radial velocity (v_R) is given in units of kilometers per second (km/s), to convert the above fraction of the speed of light (v/c) into km/s multiply by the speed of light in km/s:  c = 300,000 km/s}

2.  note the convention that if the light is "blue-shifted", (l-l_o) has a negative value since the observed wavelength (l) is smaller than the rest wavelength (l_o) and the calculated line-of-site velocity or radial velocity of the object is also negative, if the light is "red-shifted" the calculated radial velocity is positive; ("blue-shift" = neg. radial vel. = motion toward observer, "red-shift" = pos. radial vel. = motion away from observer)

1.  a star's intrinsic motion through space causes it to change position with respect to other stars on the sky.  The component of a star's velocity perpendicular to our line of sight to the star causes an angular rate of change in position as seen on the sky.  This (extremely slow!) angular motion across the sky is called proper motion(m); the units of proper motion are arcsec/year and as noted above the motion is very small, the larges know proper motion is that of Barnard's Star which has a motion of 10.3"/year

2.  relationship between a star's transverse velocity (velocity perpendicular to our line of sight) and its proper motion:

where v_T = transverse velocity in km/s, m = proper motion in arcsec/yr, r = distance to star in parsecs, (note:  the constant in parenthesis is a conversion factor so that the transverse velocity is in km/s when proper motion is in arcsec/yr and distance is expressed in pc)

1.  the space velocity (v_*) of a star is the speed and direction of motion of a star through space relative to the Sun; the space velocity can be determined by measuring the distance, proper motion, and radial velocity of a star;  the distance and proper motion determines the tranverse velocity (speed and direction in the plane of the sky) and the radial velocity gives the speed in the direction perpendicular to the plane of the sky (line of sight direction)

2.  the space velocity magnitude (speed) is then:

where all speeds are in km/s; the direction is determined by the components of the transverse velocity in the plane of the sky and the radial velocity componet