EXPERIMENTAL AND QUASI-EXPERIMENTAL DESIGNS
.
By Barry D. Friedman
Professor of Political Science
University of North Georgia
.
March 6, 2019
.
.
You might be intrigued by this anecdote (told by Peacock):
One day when I was a junior medical student, a very important Boston surgeon visited the school and delivered a great treatise on a large number of patients who had undergone successful operations for vascular reconstruction. At the end of a lecture, a young student at the back of the room timidly asked, “Do you have any controls?” Well, the great surgeon drew himself up to his full height, hit the desk, and said, “Do you mean did I not operate on half of the patients?” The hall grew very quiet then. The voice at the back of the room very hesitatingly replied, “Yes, that’s what I had in mind.” Then the visitor’s fist really came down as he thundered, “Of course not. That would have doomed half of them to their death.” G·d, it was quiet then, and one could scarcely hear the small voice ask, “Which half?”
The classic experimental design is the Cadillac of all research approaches related to the scientific method.
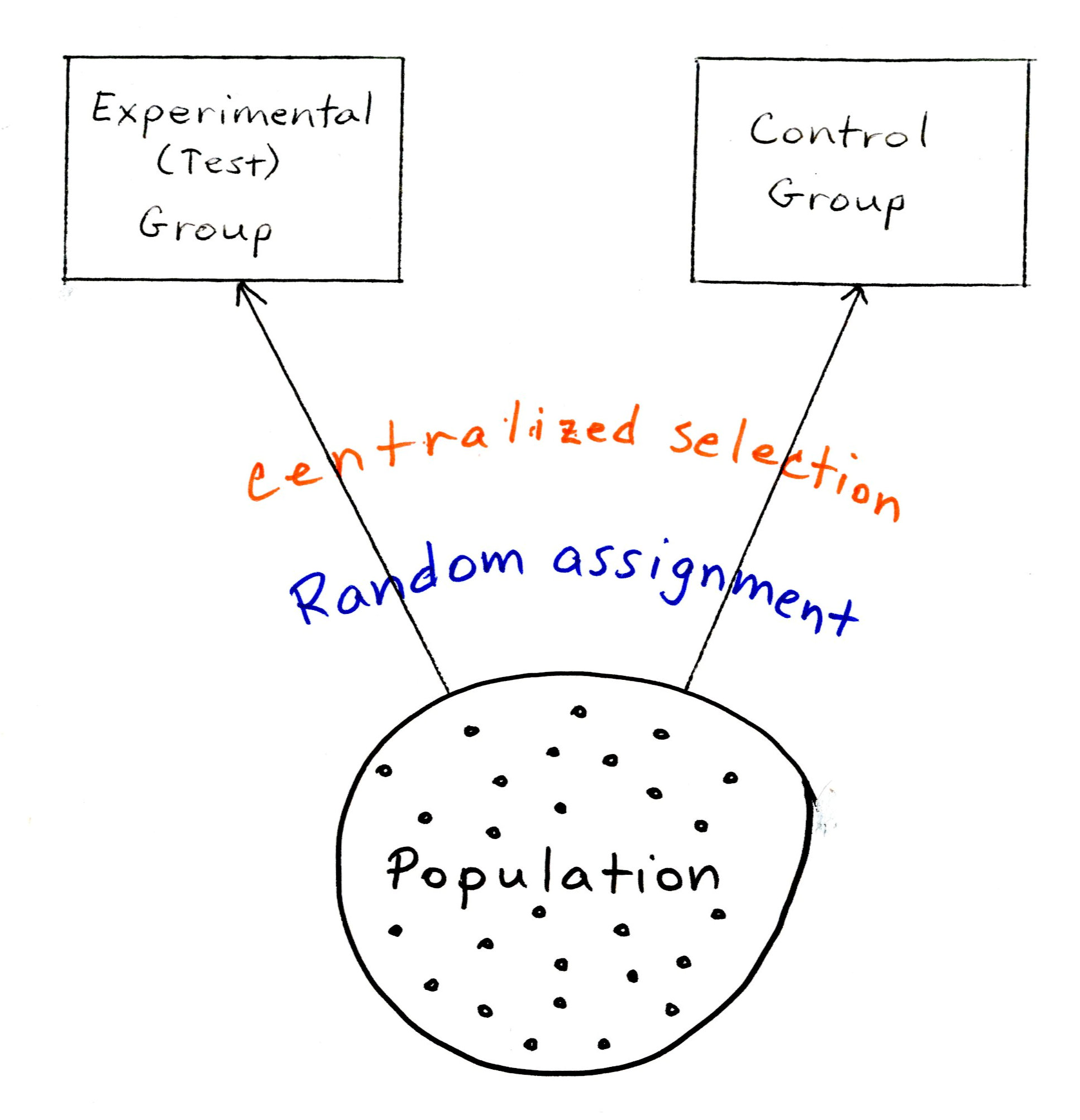
From a population, we randomly select two groups: the experimental (test) group and the control group. This is depicted in this figure:

Please note: Random selection is the hallmark of the experimental design.
An experiment has an independent variable (x) and a dependent variable (y). The independent variable (x) is the treatment.
This set of words and symbols shows the experiment’s protocol:
Experimental ® ῩT1 X ῩT2
Control ® ῩC1 ῩC2
That indicates that the two groups were selected randomly (“®”).
.
Presumably, the effect of the treatment on the dependent variable is ῩT2 - ῩC2.
The experimental design works very well if:
● The researchers are able to get information about all of the members of the population.
● The researchers are able to make contact with every person who was selected at random.
● All of the selected subjects agree to participate, show up for the experiment, cooperate with the protocol, and stay until the end (there are no drop-outs‑‑i.e., there is no attrition).
Those things virtually never happen in real life. Therefore, the vast majority of legitimate social-science research uses what are called quasi-experimental designs.
QUASI-EXPERIMENTAL DESIGN
In the case of almost all social-science research studies, we can’t randomly select participants and/or we can’t isolate them from all environmental factors.
Example: We want to test the effect of child abuse on children. A real experiment would require that we take a population of children, randomly assign participants to an experimental group and a control group, isolate them from the environment, abuse the members of the experimental group, and then attribute the difference to the treatment (abuse). Result: We’d end up in jail.
What we do instead is find abused children, try to get information about their backgrounds, and try to compare them with non-abused children.
Abused ῩT1 X ῩT2
Non-abused ῩC1 ῩC2
We will compare ῩT2 and ῩC2 , but we understand that ῩT1 may have been very different from ῩC1 and the result of X might not simply be ῩT2 - ῩC2 .
Examples of quasi-experimental design:
.
Before-after design

Notice that there is only one sample group: the test group. A pretest measurement occurs at Time 1 (before the treatment) and a posttest measurement occurs at Time 2 (after the treatment). We estimate that the effect of the treatment is T2 - T1.
.
.
Comparative post-test

This time, there are two sample groups: a test group and a control group. A pretest measurement was not done for either group. Our estimate of the effect of the treatment is T2 - C2.
.
.
Comparative change

The comparative change approach is very similar to the experimental design; the major difference is that there is no random sampling (i.e., no “®”).
.
.
Interrupted time series

In this quasi-experimental design, there is only one group: a test group. Some plural number of observations are made before the treatment and some plural number of observations are made after the treatment.
.
.
Comparative time series

This is like the interrupted-time-series design, except that now we have two sample groups.
.
.
The quasi-experimental design involves many threats to validity (internal and external): attrition, history, Hawthorne effect, maturation, regression to the mean, etc.
.
.
.
Personal disclaimer: This page is not a publication of the University of North Georgia and UNG has not edited or examined the content of the page. The author of the page is solely responsible for the content.
Last updated on March 6, 2019, by Barry D. Friedman.
Return to Barry Friedman's home page . . .